https://www.acmicpc.net/problem/21071
21071번: Long Grid Covering
We have a grid of height $3$ and width $n$, as well as pieces that occupy $3$ adjacent cells. Given $n$, determine the number of ways to fill the grid so that each cell is covered by exactly one piece and no piece sticks out of the grid. Here there is an e
www.acmicpc.net
이 문제는 상당히 어려웠다고 생각이 듭니다.
이 문제를 풀기 위해서 우선 다음 문제를 풀 필요가 있습니다.
2021.07.30 - [분할 정복을 이용한 거듭제곱/행렬 거듭제곱] - 백준 13976번: 타일 채우기 2
그런데 타일 채우기 문제와는 좀 다른 것이, 블럭의 모양새가 "ㄱ" 모양으로 생긴 것과 세 칸짜리 "1" 모양 하나가 있습니다.
이에 따라 규칙을 찾으려면 좀 많이 연구해야 합니다. 저는 $N=4$ 까지 모두 나열하고, 이후부터는 적당히 끼워 맞췄습니다..
일단 $N$ 값에 따라 최대한 모든 경우의 수를 그려보겠습니다. $\left ( N \leq 4 \right )$
$N=1$ 일 때는 한 가지 뿐입니다.
그러면 $N=2$ 일 때를 그려보겠습니다.

이제 $N=3$ 일 때를 그려보겠습니다. 그런데 경우의 수가 좀 많습니다.


일반적인 타일 채우기 문제는 이정도까지 하면 점화식을 찾기 수월하지만, 이 문제의 "odd" 개수는 매우 변칙적입니다.
odd 라는 건 일반적인 경우와 좀 이질적으로 생긴 그림들을 말하는데, 이 문제에서는 $N > 3$ 부터 등장할 것입니다.
일단 $N=4$ 일 때의 모든 경우의 수를 한 번 소개해보겠습니다.





일단 odd를 제외한 21가지 경우의 수를 모두 소개했습니다. 이제 다음으로는 odd입니다.
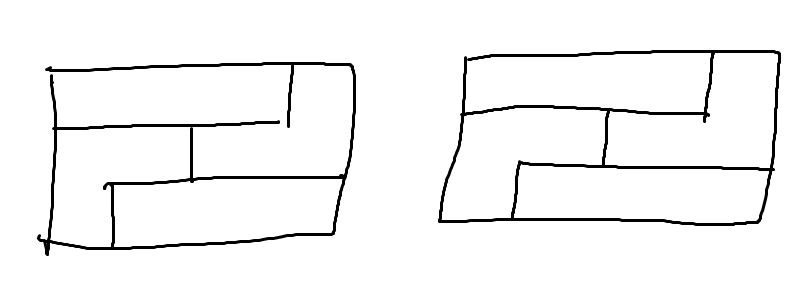
이렇게 $N=4$ 일 때는 odd가 2개입니다.
그래서 $N=4$ 일 때는 총 23가지의 경우의 수가 있습니다.
이제 $N=5$ 일 때를 소개하려는데, 이게 하나하나 그리기에는 너무 많습니다.
그러니까 적당히 유형 별로 분류해서 경우의 수를 도출하겠습니다.
$\left ( 1 \; 1 \; 1 \; 1 \; 1 \right ) \rightarrow 1$
$\left ( 1 \; 1 \; 1 \; 2 \right ) \rightarrow 4 \times 2 = 8$
$\left ( 1 \; 1 \; 3 \right ) \rightarrow 3 \times 5 = 15$
$\left ( 1 \; 2 \; 2 \right ) \rightarrow 3 \times 2 \times 2 = 12$
$\left ( 1 \; 4 \right ) \rightarrow 2 \times 2 = 4$
$\left ( 2 \; 3 \right ) \rightarrow 2 \times 5 \times 2 = 20$
중복을 잘 제거해보면 위의 60가지를 얻을 수 있습니다.
여기에 odd 가 2가지 있습니다. 그림으로 보여드리면 다음과 같습니다.

그래서 $N=5$ 일 때의 경우의 수는 총 62가지입니다.
그런데 $N=6$ 일 때는 이마저도 어렵습니다. 그래서 이제는 점화식 스러운 접근을 해야 합니다.
여기서 13976번을 응용하는 것입니다. 우선 다음을 도입하겠습니다.
$A \left ( X \right )$ : $3 \times X$ 길이의 블록을 가장 왼쪽에서부터 채우는 경우의 수
그러면 기존의 $N=5$ 의 답을 $A \left ( X \right )$ 을 이용하여 재해석 해보겠습니다.
$$A\left ( 5 \right ) = A \left ( 4 \right )+2A \left ( 3 \right )+5A \left ( 2 \right )+2A \left ( 1 \right)+2$$
이제 다시 $X=6$ 일 때에 대해 다음을 알 수 있습니다.
$$A\left ( 6 \right ) = A \left ( 5 \right ) + 2A \left ( 4 \right ) + 5A \left ( 3 \right ) +2A \left ( 2 \right ) + 2A \left ( 1 \right ) + odd \left ( 6 \right )$$
그러면 $N=6$ 일 때의 odd 개수인 $odd \left ( 6 \right )$ 을 구해야 합니다. 이는 다음과 같습니다.

그래서 $A \left ( 6 \right ) = 170$ 입니다.
이쯤에서 $A \left ( X \right )$ 을 일반화 해보겠습니다.
일단 $X$ 라는 길이를 구성하기 위해 왼쪽부터 $X-1$ 의 길이를 구성하는 경우라면 다음을 얻습니다.
$$A\left ( X \right ) \leftarrow A\left ( X-1 \right )$$
이제 $X-2$ 의 길이를 먼저 구성하면 다음을 얻습니다.
$$A\left ( X \right ) \leftarrow 2 \times A\left ( X-2 \right )$$
이는 $N=2$ 인 경우의 삽화에서 세로로 절반씩 쪼갰던 그림을 제외한 게 2가지이기 때문입니다.
이제 $X-3$ 을 먼저 구하면 어떨까요?
$N=3$ 인 경우의 10가지 경우를 모두 봤을 때, 세로로 3칸 짜리 그림이 없는 것은 5가지입니다.
따라서 다음을 얻을 수 있습니다.
$$A\left ( X \right ) \leftarrow 5 \times A \left ( X-3 \right )$$
그 이상의 경우는, odd의 개수에 의존할 수밖에 없습니다. 따라서 최종적으로 다음을 얻을 수 있습니다.
$$A\left ( X \right ) = A\left ( X-1 \right ) + 2A \left ( X-2 \right ) + 5A \left ( X-3 \right ) + \sum_{k=4}^{X-1} odd\left ( k \right ) \times A\left ( X-k \right ) + odd\left ( X \right )$$
이제 $N=7$ 인 경우를 검증해보겠습니다.
$$A\left ( 7 \right ) = A\left ( 6 \right ) + 2A \left ( 5 \right ) + 5A \left ( 4 \right ) + \sum_{k=4}^{6} odd\left ( k \right ) \times A\left ( 7-k \right ) + odd\left ( 7 \right )$$
여기서 $odd\left ( 7 \right )$ 은 얼마일까요? 그려봤습니다.

그래서 $odd\left ( 7 \right ) = 2$ 이며 $A\left ( 7 \right )=441$ 임을 알 수 있습니다.
$N=8$ 인 경우는 어떻게 될까요? 일단 기본 공식에 따라서 다음을 얻습니다.
$$A\left ( 8 \right ) = A\left ( 7 \right ) + 2A \left ( 6 \right ) + 5A \left ( 5 \right ) + \sum_{k=4}^{7} odd\left ( k \right ) \times A\left ( 8-k \right ) + odd\left ( 8 \right )$$
여기서 odd의 개수는? 제가 $N \leq 8$ 까지는 그려놨습니다.

그러니까 $A \left ( 8 \right ) = 1173$ 입니다.
언제까지 odd 개수를 그려봐야만 알 수 있을까요? 이제 odd 개수의 규칙성도 찾아봅시다.
일단 odd의 생김새부터 분석해야 합니다. 사실, $N=4$ 일 때와 $N=7$ 일 때의 odd를 비교해보세요.
그리고 $N=5$ 일 때와 $N=8$ 일 때의 odd를 비교해보세요.
odd라는 건 결국 $4 \leq N \leq 6$ 일 때의 odd 들을 기본 도형으로 해서, 가로 3칸을 더하는 것에 불과한 게 아닐까요?
이걸 증명할 방법은 저는 갖고 있지 않습니다. 다만 이 추측에 따르면 $odd \left ( X \right )$ 에는 다음과 같은 규칙이 있음을 알 수 있습니다.
$$odd\left ( X \right) = 2 \; , 2 \; , 4 \; , 2 \; , 2 \; , 4 \; , \cdots \left ( X \geq 4 \right )$$
이제 $A \left ( 9 \right )=3127$ 임을 알 수 있습니다.
아무튼, 위 추측이 참이라는 전제 하에 $A$ 값을 이제 공식을 확실히 얻었습니다. 그런데 이 공식의 크기는 $X$ 값에 비례합니다.
시간 복잡도를 위해서는 이를 줄여야 합니다. 일단 충분히 큰 $X$ 값에 대해 $A\left ( X \right)$ 을 공식을 통해 산출해봅시다.
$$A\left ( X \right ) = A\left ( X-1 \right ) + 2A\left ( X-2 \right ) + 5A\left ( X-3 \right )$$
$$+ 2A\left ( X-4 \right ) + 2A\left ( X-5 \right ) + 4A\left ( X-6 \right )$$
$$+ \ddots$$
4번째 항부터 계수가 2, 2, 4가 반복됨을 볼 수 있습니다. 그게 우리의 전제였기도 하죠.
그런데 이대로는 보기가 힘드니까, 다음을 도입하겠습니다.
$$B\left ( X \right ) = A \left ( X \right ) + A \left ( X-1 \right ) - A \left ( X-3 \right )$$
그러면 $A\left ( X \right )$ 의 점화관계에 의해 다음을 알 수 있습니다.
$$B\left ( X \right ) = 2A\left ( X-1 \right ) + 2A\left ( X-2 \right ) + 4A\left ( X-3 \right )$$
$$+ 2A\left ( X-4 \right ) + 2A\left ( X-5 \right ) + 4A\left ( X-6 \right )$$
$$+ \ddots$$
여기서도 사실 13976번의 풀이를 조금 참고해도 좋습니다. $B\left ( X \right )$ 의 정의에 따라 다음을 얻습니다.
$$B\left ( X+3 \right ) - B\left ( X \right ) = 2A\left ( X+2 \right ) + 2A\left ( X+1 \right ) + 4A\left ( X \right)$$
이를 풀게 되면 다음 식을 유도할 수 있습니다.
$$A \left ( X+3 \right) + A\left ( X+2 \right ) - 2A\left ( X+1 \right ) - 6A\left ( X \right ) - A\left ( X-1 \right ) + A\left ( X-3 \right) = 0$$
이제 점화식이 겨우 6개의 항만으로 커팅되었습니다!!!
점화식이 잘 커팅되긴 했는데, 우리는 $n$ 값이 $10^{18}$ 까지 주어지기 때문에 행렬의 거듭제곱을 써야 합니다.
(혹은 kitamasa 라든지, 다른 방법을 더 쓸 수 있다고는 합니다.)
일단 우리가 구한 점화식을 행렬로 옮겨쓰면 다음과 같음을 알 수 있습니다.
$$\begin{bmatrix} A\left ( N+3 \right ) \\ A\left ( N+2 \right ) \\ A\left ( N+1 \right ) \\ A\left ( N \right ) \\ A\left ( N-1 \right ) \\ A \left ( N-2 \right ) \end{bmatrix} = \begin{bmatrix} 1 & 2 & 6 & 1 & 0 & -1 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} A\left ( N+2 \right ) \\ A\left ( N+1 \right ) \\ A\left ( N \right ) \\ A\left ( N-1 \right ) \\ A\left ( N-2 \right ) \\ A \left ( N-3 \right ) \end{bmatrix}$$
지금까지의 아주 긴 과정을 거쳐서, 우리는 결국 다음을 얻습니다.
$$\begin{bmatrix} A\left ( N+3 \right ) \\ A\left ( N+2 \right ) \\ A\left ( N+1 \right ) \\ A\left ( N \right ) \\ A\left ( N-1 \right ) \\ A \left ( N-2 \right ) \end{bmatrix} = \begin{bmatrix} 1 & 2 & 6 & 1 & 0 & -1 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{bmatrix} ^{N-3} \begin{bmatrix} A\left ( 6 \right ) \\ A\left ( 5 \right ) \\ A\left ( 4 \right ) \\ A\left ( 3 \right ) \\ A\left ( 2 \right ) \\ A \left ( 1 \right ) \end{bmatrix}$$
이는 시간 복잡도 $O\left ( T \log N \right )$ 으로 풀 수 있습니다.
음수 모듈러 연산에 주의하여 구현하면 정답을 얻을 수 있습니다. 제 코드는 다음과 같습니다.
/*
* Author : thdtjdals3
* Date : 2021-12-23
* Description : BOJ 21071
* Link : https://www.acmicpc.net/problem/21071
*/
#include <stdio.h>
#define mod 1000000007
typedef struct {
long long array[6][6];
} Matrix;
Matrix matrix_multiply_modular (Matrix A, Matrix B);
Matrix matrix_power_modular (Matrix A, long long P);
long long simple[] = {0, 1, 3, 10, 23, 62, 170};
int main() {
int t;
scanf("%d", &t);
while(t--)
{
long long n;
scanf("%lld", &n);
if (n <= 6)
{
printf("%lld\n", simple[n]);
continue;
}
Matrix Base =
{{
{ 1, 2, 6, 1, 0, mod - 1},
{ 1, 0, 0, 0, 0, 0 },
{ 0, 1, 0, 0, 0, 0 },
{ 0, 0, 1, 0, 0, 0 },
{ 0, 0, 0, 1, 0, 0 },
{ 0, 0, 0, 0, 1, 0 }
}};
Base = matrix_power_modular(Base, n - 3);
long long answer = 0;
for (int i = 0; i < 6; i++)
{
answer = (answer + Base.array[3][i] * simple[6 - i]) % mod;
}
printf("%lld\n", answer);
}
return 0;
}
Matrix matrix_multiply_modular (Matrix A, Matrix B)
{
Matrix result = { {{0}} };
for (int i = 0; i < 6; i++)
{
for (int j = 0; j < 6; j++)
{
for (int k = 0; k < 6; k++)
{
result.array[i][j] += A.array[i][k] * B.array[k][j];
}
result.array[i][j] %= mod;
}
}
return result;
}
Matrix matrix_power_modular (Matrix A, long long P)
{
Matrix result = { {{0}} };
for (int i = 0; i < 6; i++)
{
result.array[i][i] = 1;
}
while(P > 0)
{
if (P % 2)
{
result = matrix_multiply_modular (result, A);
}
A = matrix_multiply_modular (A, A);
P /= 2;
}
return result;
}(C11, 0ms, 1116KB, 제출번호 36607312)
이 문제는 정말 어려웠습니다. 만약 초기 몇 항의 값을 알 수 없었다면 크게 곤란했을 것입니다.
그러므로 초반 몇 항의 mod $10^{9}+7$ 값을 저도 공개하고자 합니다.
| $n$ 의 값 | 정답 |
| 1 | 1 |
| 2 | 3 |
| 3 | 10 |
| 4 | 23 |
| 5 | 62 |
| 6 | 170 |
| 7 | 441 |
| 8 | 1173 |
| 9 | 3127 |
| 10 | 8266 |
| 11 | 21937 |
이외 다른 항의 값들과 kitamasa / Berlekamp-Massey를 쓰는 접근법을 다음 링크에서 소개하고 있습니다.
https://blog.naver.com/PostView.naver?blogId=jinhan814&logNo=222445242893
'분할 정복을 이용한 거듭제곱 > 행렬 거듭제곱' 카테고리의 다른 글
| 백준 11333번: 4×n 타일링 (0) | 2022.05.01 |
|---|---|
| 백준 17539: Keep Calm and Sell Balloons (0) | 2022.01.20 |
| 백준 12987번: Matrix Again (0) | 2021.12.21 |
| 백준 23819번: 묻고 더블로 마셔 (1) | 2021.12.21 |
| 백준 15570번 : 블록 2 (0) | 2021.12.17 |